Test design techniques
Let’s think about quality control basics for a moment. In my opinion this is the most important thing to be able to design the right test case. No matter if this is automated or manual we need to get the confidence software we are working on has a very low probability of still unrevealed functional defects in the area covered by our test cases. We do not have to reinvent the wheel as we have already test design techniques there in place to help us achieve this goal. Because it is basics of the basics for QA engineer you know all of them and apply them in practice aren’t you… ? I can tell you basing on my interview experience in reality the majority of QA engineers heard about some of them but also majority is not applying them in practice (as described here). If you are by any chance in this notorious majority, I hope you read all this no to be part of this group of people anymore.
Pair wise testing
I would like to concentrate in this article on the most advanced test design technique in my opinion, or at least most interesting from my point of view which is pair-wise testing. The purpose of this technique is to deal with situation when number of combinations we have to test is too large. Because we have combinations almost everywhere this is extremly important thing to know. The of combinatorial testing problems are for example:
- application setting page with many switches (we need to know if some combination of settings we choose doesn’t influence any of them – Notepad++ preferences),
- software designed for many platforms (the combination is here array of operating systems – UNIX, mobile, Windows – and external software combinations – database vendors, database providers),
- aplication which has REST or SOAP web service interface (number of available combination of input data – application accepts POST message in XML format, some of the elements are mandatory, some of them are optional)
The idea behind pair-wise technique is to focus on pairs instead of all combinations.
For example, let’s imagine we have 3 inputs where each of them accepts one letter at a time. 1. input accepts only letters (A,B), 2. (A,B) and 3. (A,B,C). We can easily write all combinations for such model (2x2x3=12 combinations):
1 => (A,B)
2 => (A,B)
3 => (A,B,C)
| no | 1 | 2 | 3 |
|---|---|---|---|
| 1 | A | A | A |
| 2 | A | A | B |
| 3 | A | A | C |
| 4 | A | B | A |
| 5 | A | B | B |
| 6 | A | B | C |
| 7 | B | A | A |
| 8 | B | A | B |
| 9 | B | A | C |
| 10 | B | B | A |
| 11 | B | B | B |
| 12 | B | B | C |
Of course, in such a case we do not need any special approach, we can test all of them. But let’s think of a situation each combination takes 1 week to execute or else that we have 3 inputs where range A-Z is accepted or when each input accepts more then one letter.
We can decrease the coverage for 100% (all combinations) to all pairs. Please notice 100% coverage here means actually all triplets. We are actually moving from all triplets to all pairs now:
Let’s enumerate all pair combinations as we are interested now only in pairs:
| no | 1 | 2 | 3 |
|---|---|---|---|
| 1 | A | A | – |
| 2 | A | B | – |
| 3 | B | A | – |
| 4 | B | B | – |
| 5 | A | – | A |
| 6 | A | – | B |
| 7 | A | – | C |
| 8 | B | – | A |
| 9 | B | – | B |
| 10 | B | – | C |
| 11 | – | A | A |
| 12 | – | A | B |
| 13 | – | A | C |
| 14 | – | B | A |
| 15 | – | B | B |
| 16 | – | B | C |
Let’s choose the subset of combinations which will have all the pairs listed above. Consider this:
| no | Comb. | 1 | 2 | 3 | comment |
|---|---|---|---|---|---|
| 1 | AAA | AA_ | _AA | A_A | we don’t need this, we have these pairs in AAC, BAA and ABA |
| 2 | AAB | AA_ | _AB | A_B | we don’t need this, we have these pairs in AAC, BAB and ABB |
| 3 | AAC | AA_ | _AC | A_C | |
| 4 | ABA | AB_ | _BA | A_A | |
| 5 | ABB | AB_ | _BB | A_B | |
| 6 | ABC | AB_ | _BC | A_C | |
| 7 | BAA | BA_ | _AA | B_A | |
| 8 | BAB | BA_ | _AB | B_B | |
| 9 | BAC | BA_ | _AC | B_C | we don’t need this, we have these pairs in BAB, AAC and BBC |
| 10 | BBA | BB_ | _BA | B_A | we don’t need this, we have these pairs in BBC, ABA and BAA |
| 11 | BBB | BB_ | _BB | B_B | we don’t need this, we have these pairs in BBC, ABB and BAB |
| 12 | BBC | BB_ | _BC | B_C |
So, we can use now just 7 combinations out of 12 originally:
| no | Comb. | 1 | 2 | 3 | comment |
|---|---|---|---|---|---|
| 1 | AAC | AA | _AC | A_C | |
| 2 | ABA | AB | _BA | A_A | |
| 3 | ABB | AB | _BB | A_B | |
| 4 | ABC | AB | _BC | A_C | |
| 5 | BAA | BA | _AA | B_A | |
| 6 | BAB | BA | _AB | B_B | |
| 7 | BBC | BB | _BC | B_C |
Can we reduce number of combinations more? Yes, we can move from all pairs coverage to single value which would mean that we want to use every possible value for each input at least once and we do not care about any combinations at the same time:
| no | 1 | 2 | 3 |
|---|---|---|---|
| 1 | A | A | A |
| 2 | B | B | B |
| 3 | A | B | C |
In this set of 3 combinations input 1 uses A and B, 2 uses A and B and 3 uses A, B and C which is all that we need.
As you can see we have a nice theory, but we are not going to compute things manually, are we ?
TCases
Let’s use the software for the example from the previous section.
It is named TCases and it is located HERE. I will not be explaining the usage as there is excellent help on the page there (I tell you it is really excellent). It is enough to just say we need input file which is modelling the input and generator file which allows us to set actual coverage. The input file for the example shown above looks like this:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
<?xml version="1.0"?> <System name="example"> <Function name="abc"> <Input type="arg"> <Var name="input1"> <Value name="A"/> <Value name="B"/> </Var> </Input> <Input type="arg"> <Var name="input2"> <Value name="A"/> <Value name="B"/> </Var> </Input> <Input type="arg"> <Var name="input3"> <Value name="A"/> <Value name="B"/> <Value name="C"/> </Var> </Input> </Function> </System> |
After we say we want to have single value coverage (which is called 1-tuple coverage):
|
1 2 3 |
<Generators> <TupleGenerator tuples="1"/> </Generators> |
We get the same result as we did manually:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
<?xml version="1.0"?> <TestCases system="example"> <Function name="abc"> <TestCase id="0"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="1"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="2"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="C"/> </Input> </TestCase> </Function> </TestCases> |
It doesn’t matter 3. test case is different as the only thing which matters there is to use C for the 3. input.
Now, let’s repeat all pairs coverage (named 2-tuple coverage):
|
1 2 3 |
<Generators> <TupleGenerator tuples="2"/> </Generators> |
The result is:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
<?xml version="1.0"?> <TestCases system="example"> <Function name="abc"> <TestCase id="0"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="1"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="2"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="C"/> </Input> </TestCase> <TestCase id="3"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="B"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="4"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="A"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="5"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="C"/> </Input> </TestCase> <TestCase id="6"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="A"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="7"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="B"/> <Var name="input3" value="A"/> </Input> </TestCase> </Function> </TestCases> |
There is slight difference as number of test cases here is 8 while it was 7 when done manually. This is because TCases by default doesn’t guarantee minimal set of pair combinations. We need to explicitly ask for it by using tcases-reducer (I must say I overlooked it initially – many thanks to Kerry Kimbrough for helping me with this). Looking at this result we can see we need to exclude AAA from this set as the pairs from AAA are also present in test cases id: 2 (AA_), 4 (_AA) and 7 (A_A). Let’s see what happens.
After running tcases-reducer generator file is modified:
|
1 2 3 4 5 6 7 |
<?xml version="1.0"?> <Generators> <TupleGenerator function="*" tuples="2"> </TupleGenerator> <TupleGenerator function="abc" seed="1374626318301314048" tuples="2"> </TupleGenerator> </Generators> |
After running tcases with new generator the result is surprising:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
<?xml version="1.0"?> <TestCases system="example"> <Function name="abc"> <TestCase id="0"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="1"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="C"/> </Input> </TestCase> <TestCase id="2"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="B"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="3"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="A"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="4"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="5"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="C"/> </Input> </TestCase> </Function> </TestCases> |
Wait a minute, we have only 6 combinations, how is this possible?
Let’s combine manual table I created previously with this one:
| no | Comb. | 1 | 2 | 3 | AUTO COMB | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|---|
| 1 | AAC | AA_ | _AC | A_C | AAC | AA_ | _AC | A_C |
| 2 | ABA | AB_ | _BA | A_A | ABA | AB | _BA | A_A |
| 3 | ABB | AB_ | _BB | A_B | AAB | AA_ | _AB | A_B |
| 4 | ABC | AB_ | _BC | A_C | BBB | BB_ | B_B | _BB |
| 5 | BAA | BA_ | _AA | B_A | BAA | BA_ | B_A | _AA |
| 6 | BAB | BA_ | _AB | B_B | BBC | BB_ | B_C | _BC |
| 7 | BBC | BB_ | _BC | B_C |
It turns out, it is important what is the sequence in which we are choosing a combination to be left out.
TCases found a way to have only 6 combinations and to cover all pairs ! Different combinations are marked green. As I pointed out there are 16 pairs total: my manual combination set was redundant by 5 pairs and computed combinations are redundant only by 2 pairs (take a look at yellow cells).
And finally let’s change the generator to use triplets which means 100% coverage in our example:
|
1 2 3 |
<Generators> <TupleGenerator tuples="3"/> </Generators> |
Result:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
<?xml version="1.0"?> <TestCases system="example"> <Function name="abc"> <TestCase id="0"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="1"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="2"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="C"/> </Input> </TestCase> <TestCase id="3"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="B"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="4"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="A"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="5"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="C"/> </Input> </TestCase> <TestCase id="6"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="A"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="7"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="B"/> <Var name="input3" value="A"/> </Input> </TestCase> <TestCase id="8"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="A"/> <Var name="input3" value="B"/> </Input> </TestCase> <TestCase id="9"> <Input type="arg"> <Var name="input1" value="A"/> <Var name="input2" value="B"/> <Var name="input3" value="C"/> </Input> </TestCase> <TestCase id="10"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="A"/> <Var name="input3" value="C"/> </Input> </TestCase> <TestCase id="11"> <Input type="arg"> <Var name="input1" value="B"/> <Var name="input2" value="B"/> <Var name="input3" value="A"/> </Input> </TestCase> </Function> </TestCases> |
So it must be the same which is 12 combinations.
As you can see this application is working really nicely.
But what about real usage of this technique in real life testing problems? Let’s apply it!
Practice
Rarely can I find such a superb software like this. I am not sure if you are seeing the power of this tool yet. Let’s use it in practical example.
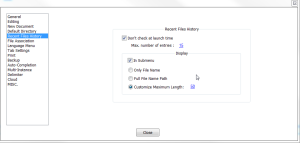
Let’s assume testing of Notepad++ “recent file history” is required.
The setting looks like this:
The input model for this testing problem can look like this:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
<?xml version="1.0"?> <System name="Notepad"> <Function name="recent_files_history"> <Input type="arg"> <Var name="launchTime_isChecked"> <Value name="yes"/> <Value name="no"/> </Var> </Input> <Input type="arg"> <Var name="numberOfEntries_isSetTo"> <Value name="0"/> <Value name="15"/> </Var> </Input> <Input type="arg"> <VarSet name="display"> <Var name="inSubmenu_isSelected"> <Value name="yes"/> <Value name="no"/> </Var> <Var name="configuration_isSetTo"> <Value name="only_filename"/> <Value name="file_full_name_path"/> <Value name="customize_maximum_length" property="custom"/> </Var> <Var name="customSize_isSetTo" when="custom"> <Value name="0"/> <Value name="15"/> <Value name="10"/> </Var> </VarSet> </Input> </Function> </System> |
Take a look at customSize_isSetTo – this is dependent variable which is related to customize_maximum_length value of configuration_isSetTo variable.
Now, the simplest test suite with 1-tuple coverage looks like this:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
<?xml version="1.0"?> <TestCases system="Notepad"> <Function name="recent_files_history"> <TestCase id="0"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="only_filename"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="1"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="file_full_name_path"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="2"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="0"/> </Input> </TestCase> <TestCase id="3"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="15"/> </Input> </TestCase> <TestCase id="4"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="10"/> </Input> </TestCase> </Function> </TestCases> |
Custom size is set to NA when maximum length is not customized in the test case. This is really important to process dependent variables.
And 2-tuple coverage:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 |
<?xml version="1.0"?> <TestCases system="Notepad"> <Function name="recent_files_history"> <TestCase id="0"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="only_filename"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="1"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="file_full_name_path"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="2"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="0"/> </Input> </TestCase> <TestCase id="3"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="15"/> </Input> </TestCase> <TestCase id="4"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="10"/> </Input> </TestCase> <TestCase id="5"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="file_full_name_path"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="6"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="15"/> </Input> </TestCase> <TestCase id="7"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="only_filename"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="8"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="0"/> </Input> </TestCase> <TestCase id="9"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="10"/> </Input> </TestCase> <TestCase id="10"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="file_full_name_path"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="11"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="only_filename"/> <Var name="display.customSize_isSetTo" value="NA"/> </Input> </TestCase> <TestCase id="12"> <Input type="arg"> <Var name="launchTime_isChecked" value="no"/> <Var name="numberOfEntries_isSetTo" value="15"/> <Var name="display.inSubmenu_isSelected" value="yes"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="15"/> </Input> </TestCase> <TestCase id="13"> <Input type="arg"> <Var name="launchTime_isChecked" value="yes"/> <Var name="numberOfEntries_isSetTo" value="0"/> <Var name="display.inSubmenu_isSelected" value="no"/> <Var name="display.configuration_isSetTo" value="customize_maximum_length"/> <Var name="display.customSize_isSetTo" value="0"/> </Input> </TestCase> </Function> </TestCases> |
We can know decide if we have enough resources to process 1-tuple or 2-tuple coverage. We need to concentrate only on proper model input to have confidence we are achieving the right coverage. What is also important we have documented the way of creating test cases.
It is a giant leap towards the right coverage.